[R] 의사결정나무, decision tree | rpart::rpart()
하단의 목차를 클릭하여 이동할 수 있습니다 :)
1. 의사결정나무
1-1. 의사결정나무의 구조
1-2. 알고리즘 요약
2. 분할 (CART 기준)
2-1. 목적 함수 (Objective function)
2-2. 실제 예 (회귀 & 분류)
3. 튜닝
3-1. Early stopping (조기 종료)
3-2. Pruning
4. R 실습 (의사결정나무 분석)
4-1. rpart::rpart()
4-2. 모델 적용
4-3. 의사결정나무 시각화 (rpart.plot())
4-4. 1-SE rule (cp($\alpha$)값에 따른 가지치기 결정)
5. caret을 통한 예측모델 모델링하기
5-1. Modeling
5-2. 시각화를 통한 결과 해석
6. 번외 (회위 & 이항분류)
7. Reference
1. 의사결정나무
- 의사결정나무는 비모수적 알고리즘이다.
- 의사결정나무는 분할 규칙(splitting rules)에 따라 특성 공간을 반응값이 유사하고, 겹치지 않는 작은 영역으로 나눈다.
- 쉽게 말하면 분류를 할 경우 분할 규칙에 따라 최대한 같은 범주끼리 묶으며, 회귀를 할 경우 규칙에 따라 최대한 같은 범위의 수끼리 묶이도록 한다.
- 장단점
- 장점
- 간단한 기준을 통해 분할 및 정복(divide-and-conquer)하기에 알고리즘을 해석하기 쉽다.
- 마찬가지로 tree diagrams을 통해 알고리즘을 시각화하여 확인하기도 편하다.
- 단점
- Neural Networks 혹은 MARS(Multivariate Adaptive Regression Splines) 등 복잡한 알고리즘에 비하여 예측 성능이 떨어진다.
- 장점
1-1. 의사결정나무의 구조

- Root node : 분할의 시작점으로 모든 training data를 내포하고 있다.
- Internal node : Leaf node와 Root node 사이의 모든 node를 의미한다.
- Branch : 각 nodes를 연결하는 가지를 의미한다.
- Leaf node : 분할이 완료된 최종 node로 예측값을 내포하고 있다.
1-2. 알고리즘 요약
- Decision tree를 구축하는 데 가장 잘 알려진 방법은 classification and regression tree (CART) 이다.
- 기본적으로 decision tree는 결과변수를 유사한 그룹으로 분할하는 것을 목표로 한다.
- 회귀 : 비슷한 수치값들 끼리 모이도록
- 분류 : 동일한 범주를 갖도록
- 최종 예측값(Leaf node)까지 분할되는 과정은 다음과 같다.
- Root node 부터 예측변수 중 하나(each feature)를 기준으로 하여 이항 분류(binary classification)를 반복한다. 단순하게 이야기하면 yes-or-no questeions를 반복한다.
- 반복이 끝나는 시점은 decision tree의 적절한 정지 기준이 만족된 때이다. (e.g. tree의 최대 깊이).
- 분할이 종료 되었다면 Leaf node에서 예측값을 출력한다. 일반적으로 예측값은 다음과 같은 방법으로 구한다.
- 회귀 : Leaf node가 내포한 데이터의 평균.
- 분류 : Leaf node가 내포한 범주들 중 최빈 범주. (예측 확률이 가장 높은 범주).
- 분류의 경우 각 Leaf node의 범주의 비율을 예측 확률로 반환할 수 있다. (로지스틱 회귀와 유사하다).

2. 분할 (CART 기준)
2-1. 목적 함수 (Objective function)
- 각 노드를 분할할 때의 목적은 가장 분할이 잘 되게(실제값과 예측값의 차이가 작게)할 수 있는 적합한 예측변수($x_i$)를 찾는 것이다.
- 다른 말로하면 목적함수를 최소화하는 분류 기준인 예측변수를 찾는다. 즉 트리의 각 노드를 분할 할 때 목적함수를 감소를 최대화 해야한다 (Maximum reduction of object function).
- Decision tree에서 실제값과 예측값의 차이를 측정하는 목적함수는 일반적으로 다음 세 가지가 있다.
회귀 : SSE

- 개별 leaf node의 SSE를 계산 뒤에 모두 합한다.
- 이때 Decision tree는 SSE의 합을 최소화하는 방향으로 분류를 한다.
분류 1 : Average Cross-Entropy

- 쉽게 설명하면 leaf node를 통해 예측한 각 범주의 확률과 개별 범주의 encoding 값을 곱하여 더한다.
- 단, log() 확률을 사용하기에 음수를 갖는다.
- 따라서 $1\over N$으로 평균냄과 동시에 '-1'을 곱하여 양수로 설정한다.
- 양수로 설정하면 목적함수를 최소화하는 과정에서 음의 무한대로 발생하는 것을 방지한다.
- 목적함수가 의미하는 것은 모델이 예측한 확률 분포와 실제 값의 차이를 측정하는 것이다.
- 이때 Decision tree는 average cross-entropy를 최소화하는 방향으로 분류한다.
분류 2 : Gini Index

- 위의 지표를 지니 불순도(Gini impurity)라고도 한다. 다시 설명하면 지니 불순도를 통해 얼마나 순수(purity)한지 평가한다.
- 단순히 개별 데이터에 대한 예측확률의 제곱을 1에서 차감한다.
- 따라서 예측확률(해당 범주일 확률)이 크다면 Gini index의 값은 작아진다.
- 목적함수를 최소화하면 Gini Index를 최소화하는 것이기에 예측확률이 높게 예측했다고 볼 수 있다. 즉, 분류가 잘 되었다 볼 수 있다.
- 이때 Decision tree는 gini index를 최소화하는 방향으로 분류한다.
P.S.
- 개별 leaf node의 예측값들은 모두 같은 값을 갖는다. 다시 이야기하면 leaf node로 분류된 데이터는 다른 예측값을 갖지 않는다.
- 일반적으로 Gini Index를 사용한다.
- 재차 강조하지만 상기된 object function이 node의 분류 결과 최대로 감소하도록 분류한다.
2-2. 실제 예 (회귀 & 분류)
- 예를 보이기 앞서 decision tree는 동일한 예측변수를 분류 기준으로 여러번 사요할 수 있다. 이는 중요한 특징 중 하나이다.
회귀

- 각 leaf node는 분류된 train set의 값들의 평균을 갖는다. 후에 dev set 혹은 test set에 모델이 적용된다면 dev set과 test set은 train set의 값을 기반으로 분류된다.
- 각 leaf node가 갖는 평균값을 기준으로 실제값과의 차이를 통해 SSE를 구한다. 그 후 전체 leaf node의 SSE를 합한다. (앞서 설명한 것과 같은 방식).
- 따라서 전체 SSE를 최소화하는 방향으로 분류를 진행하는 것이다.
- Leaf node 아래의 %(붉은 동그라미)가 의미하는 것은 해당 leaf node가 전체 data set 중 몇 %의 데이터를 내포하고 있는가이다.
- 첫 번째 leaf node는 전체 데이터 중 30%의 데이터를 내포하고 있다.
분류

- Leaf node를 확인하면 각 범주 별 예측확률을 알 수 있다. 개별 leaf node는 가장 높은 확률을 갖는 범주로 분류된다.
- 오른쪽 모자이크 플롯을 확인하면 분류결과(상자의 색)와 그에 해당하는 sample(모양이 다름)을 확인할 수 있다.
- 위와 같은 분류를 할 때에 cross-entropy 혹은 gini index를 사용하는 것이다. (주로 gini index).
3. 튜닝
- 의사결정나무를 너무 크게 성장시키면 과적합 문제가 발생할 가능성이 크다. 즉 모델의 일반화 가능성이 떨어지게 된다.
- 위와 같은 문제를 방지하기 위해 의사결정나무는 나무의 깊이와 복잡도를 균형성 있게 맞추어 줄 필요가 있다. 다음의 두 가지는 일반적으로 사용되는 방법들이다.
3-1. Early stopping (조기 종료)
Early stopping은 의사결정나무의 성장을 조기에 종료하여 적절한 의사결정나무가 생성되게 하는 방법이다. 다양한 방법들이 있지만 주로 사용되는 방법들은 tree depth와 minimum data in leaf node를 활용한다.
- Tree depth
- 명시적으로 의사결정나무의 깊이를 지정하는 방법이다.
- 일반적으로 depth가 깊어지면 모델의 분산이 커지며 과적합의 위험이 발생할 가능성이 있다.
- Minimum data in leaf node
- Leaf node가 가져야할 최소 데이터의 수를 지정한다.
- Leaf node가 가져야할 최소 데이터의 수가 크다면 분류 자체를 잘 수행하지 못하기에 과소적합의 문제가 발생할 가능성이 있다.

Maximum data in leaf node = 1인 상태에서 max depth = 15 (우측 상단)의 경우 모델의 분산이 매우 크다. 즉 과적합의 위험이 있다. Max depth = 15를 유지한 채로 maximum data in leaf node = 15 (우측 하단)의 경우 leaf node가 가져야할 최소 데이터를 증가시킴으로 인하여 분산이 줄어들었다. 그러나 데이터에 존재하는 여러 패턴을 놓칠 수 있기에 과소적함의 위험이 있다. 따라서 이 사이의 균형을 맞춰야 한다.
P.S. 주의
- caret을 이용해 예측모델을 모델링할 경우에는 위의 하이퍼 파라미터를 튜닝할 수 없다. 이유는 caret이 cp($\alpha$)만을 튜닝하도록 하기 때문이다.
- 해당 내용은 후술하는 R 실습에서 직접 확인할 수 있다.
3-2. Pruning
가지치기(Pruning)는 목적함수에 복잡도 패널티(complexity penalty, $\alpha$)를 더하여 의사결정나무 자체의 크기를 조정하는 방법이다. 복잡도 패널티라는 용어자체는 생소할 수 있지만 목적함수에 특정 수를 더하여 목적함수를 최소화하는 것을 더 어렵게 만드는 것을 의미한다. 회귀 나무의 목적함수에 복잡도 패널티를 더하면 다음과 같다.

기존의 목적함수는 분류 이전의 SSE보다 분류 이후의 SSE가 더 작은 값을 갖도록 minimize를 목적으로 하였다. 변환 후의 식 또한 목적은 동일하지만 복잡도 패널티가 추가된다. 즉 SSE의 감소정도가 복잡도 패널티보다 커야지만 분류가 이루어진다. 이를 시각적으로 정리하면 다음과 같다.

목적함수만 있는 경우에는 SSE가 감소하기만 하면 되지만 패널티가 추가된 경우에는 패널티의 증가 정도보다 SSE의 감소폭이 더 커야한다. 상기 예의 경우 SSE는 3 감소하지만 패널티가 5 증가하기에 더이상 의사결정나무를 성장시킬 필요가 없다.
$\alpha$
- $alpha$는 범위 값으로 하여 CV를 통해 최적화를 수행하는 방식으로 결정할 수 있다. 이를 통해 복잡도 패널티를 조정한다.
- 다시 말하면 $alpha$는 하이퍼 파라미터이다. (하이퍼 파라미터란 ML training에 관여하는 외부 설정 변수를 의미한다).
4. R 실습 (의사결정나무 분석)
들어가기에 앞서 R에서 제공하는 ML들은(전부는 아니지만?) encoding, cross-validation, 결측치 처리 등의 전처리를 자동적으로 수행해 준다. 단, 구체적인 분석을 원할 경우 직접 전처리를 하고 전달할 수도 있다. python과는 조금 다른 부분이기에 주의해야 한다.
P.S. ML 주의점
- 모델에서는 핵심적으로 튜닝해야하는 하이퍼 파라미터들이 있다. 따라서 중요도에 맞게 튜닝을 수행해 주는 것이 좋다.
- 의사결정나무는 "3. 튜닝"에 다루었던 인자들이 포함된다. ($\alpha$, 나무의 깊이, minimum number of leaf node).
- 단, 상술하였듯이 caret을 사용할 경우 cp 외의 다른 인자들은 튜닝이 불가하다.
- Default로 적용되는 값이 최선인 경우도 존재한다. 따라서 튜닝보다 데이터 자체에 집중(파생 변수 등)하는 것이 나은 경우도 존재한다.
4-1. rpart::rpart()
rpart(
formula,
data,
weights,
subset,
na.action = na.rpart,
method,
model = FALSE,
parms,
control,
cost,
...
)
ML 모델이기 때문에 많은 파라미터가 존재하지만 일반적으로 색을 칠해둔 파라미터만 설정하면 된다. 이외의 파라미터는 주어진 데이터에 불균형(imbalance)있는 등의 특정 상황에 활용한다. (또한 대부분의 인자는 rpart가 주어진 데이터에 맞게 자동적으로 처리한다 따라서 base model 등에서는 크게 신경 쓸 필요 없다).
- formula
- 모델에 적용할 종속변수와 예측변수를 전달한다.
- '결과변수 ~ 예측변수' 형태로 전달한다.
- data
- 의사결정나무를 적용할 데이터 프레임을 의미한다.
- weights
- 각 행별 가중치를 의미한다.
- Class에 불균형이 있는 경우 사용할 수 있다.
- 예를 들어 결과변수가 "Yes"인 경우는 2, "No"인 경우는 1을 전달한다.
- subset
- 전체 데이터 중에 일부 데이터(subset)에만 의사결정나무를 적용할 때 사용한다.
- na.action
- 결측치 처리 방식을 결정한다.
- method (rpart()가 알아서 처리한다).
- 어떤 의사결정나무를 적용할지 결정한다. (e.g. 회귀, 분류 등).
- 회귀의 경우 "anova"를, 분류의 경우 "class"를 적용한다.
- parms
- gini-index, information, 그리고 SSE 등 분할 기준이되는 목적함수를 전달한다.
- model
- 모델링된 의사결정나무의 세부 모델 사항을 반환할 것인지를 결정한다.
- control
- 따로 다루어야 하는 부분이기에 바로 하단에 후술한다.
- cost
- 오분류 비용을 정의한다. 즉 오차 행렬의 각 셀마다 가중치를 적용한다. 예를 들어 암에 걸렸지만 암환자가 아니라 진단하는 경우에 5와 같은 높은 비용을 주어 분류를 세밀하게 수행할 수 있다.
- matrix 형태로 전달한다.
P.S.많은 인자가 존재하지만 정말 간단하게는 formula와 data만을 전달하여 모델링을 할 수 있으며 필요한 경우 하이퍼 파리미터를 튜닝하기 위해 control을 전달할 수 있다.
rpart.control
rpart.control(
minsplit = 20,
minbucket = round(minsplit/3),
cp = 0.01,
maxdepth = 30,
xval = 10,
...
)
생략된 부분은 분할과 관련된 하이퍼 파라미터로 해당 포스팅에서는 Hands on machine learning with R에서 다룬 (3. 튜닝) 방식만을 다룬다.
- minsplit
- 분할되기 위해서 각 node가 가져야할 최소 데이터의 수이다.
- 예를 들어 minsplit = 20일 때 node 내에 17개의 데이터가 있다면 17 < 20 이기때문에 분할할 수 없다.
- minbucket
- 앞서 minimum number of leaf node로 leaf node가 가져야할 최소한의 데이터의 수를 의미한다.
- cp (caret으로 튜닝할 경우 유일 가능 하이퍼 파라미터)
- Complexity penalty의 약자로 앞서 다룬 $alpha$가 갖을 수 있는 최소값을 의미한다.
- $alpha$는 rpart() 자체에서 CV를 통해 튜닝을 하는데 튜닝되는 $alpha$는 cp보다 작은 값을 갖을 수 없다.
- 만약 cp = 0이라면 $alpha$는 무한히 작아진다.
- maxdepth
- 의사결정나무가 갖을 수 있는 나무의 최대 깊이이다.
- xval
- rpart()는 자동적으로 CV를 수행한다. xval은 몇 개의 데이터 셋으로 나눌 것인가를 설정한다. (e.g. xval = 10, 10개의 데이터 셋으로 CV를 수행한다).
- rpart()는 xval에 명시된 수의 데이터 셋으로 CV를 수행하며 $alpha$를 튜닝한다.
- 단, 결과변수가 갖는 클래스의 비율 등을 기준을 하지 않고 무작위로 데이터 셋을 나눈다. 따라서 예측 모델을 형성할 때에는 개별적으로 CV를 설정하고, caret을 사용하는 것이 좋다.
4-2. 모델 적용
모델을 적용할 예제 데이터는 다음 링크의 kaggle의 train.csv 데이터를 사용하였다.
https://www.kaggle.com/competitions/playground-series-s4e2/data?select=train.csv
# libraries
# Preprocessing
library(readr)
library(dplyr)
# modeling
library(rpart)
# vizualizing
library(rpart.plot)
# 데이터 불러오기---------------------------------------------------------------
# kaggle url로 읽어오지 않았기에 local 환경을 사용한다.
df <- read_csv("개별 local 환경 데이터 주소")
head(df)
summary(df)
# chr형 모두 factor로 변환
df <- df %>%
mutate(across(where(is.character), as.factor))
summary(df)
# modelding---------------------------------------------------------------------
dt1 <- rpart(NObeyesdad ~ .,
data = df,
method = "class",
# control 인자는 defualt 값으로 사용할 수도 있다.
# 원한다면 상술된 minsplit, minbucket 등도 사용할 수 있다.
control = list(cp = 0.00125, xval = 10))
dt1
P.S. control 인자는 모델링 과정에서 주지 않아도 되지만 포스팅의 실습 결과가 달라질 수 있다. (가능하면 그대로 사용).
4-3. 의사결정나무 시각화 (rpart.plot::rpart.plot())
rpart.plot패키지의 rpart.plot() 함수를 통해 생성된 의사결정나무를 확인할 수 있다. 단, 의사결정나무가 너무 큰 경우에는 출력이 불가하거나 시각화의 의미가 없어진다.
# vizualizing
library(rpart.plot)
# Decision tree 시각화----------------------------------------------------------
rpart.plot(dt1,
# 7 가지의 범주가 있기 때문에 7 가지 색을 활용한다.
box.palette = list("lightblue",
"lightgreen",
"lightcoral",
"gray",
"pink",
"yellow",
"purple"),
cex = 0.35, # 글자 수
# 출력 type을 결정할 수 있다.
# 자세한 것은 rpart.plot() document를 참고(하단 링크).
extra=5)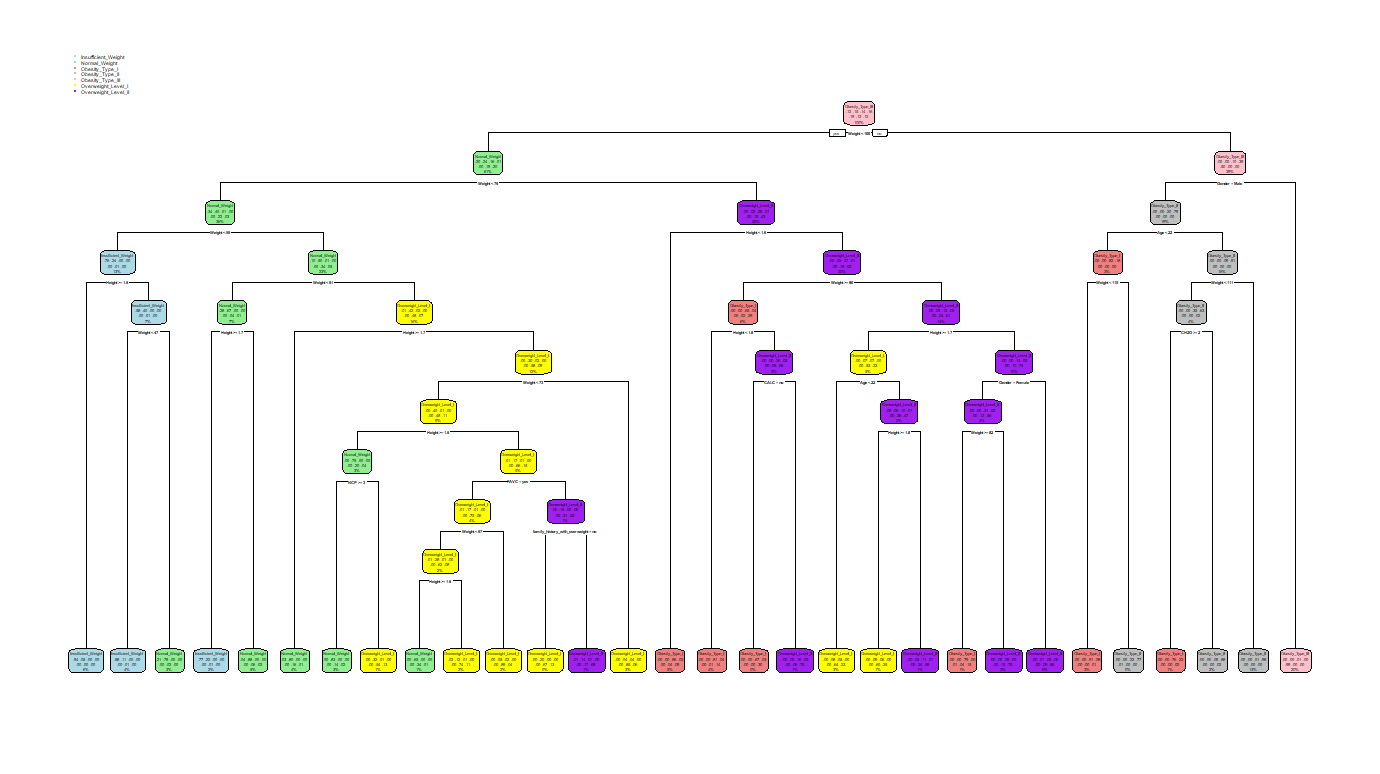
rpart.plot()에 관한 인자들은 크게 어렵지 않으며 다음의 링크에서 확인할 수 있다. (gpt가 요약을 더 잘 해준다).
https://www.rdocumentation.org/packages/rpart.plot/versions/3.1.2/topics/rpart.plot
rpart.plot function - RDocumentation
If roundint=TRUE (default) and all values of a predictor in the training data are integers, then splits for that predictor are rounded to integer. For example, display nsiblings < 3 instead of nsiblings < 2.5. If roundint=TRUE and the data used to build th
www.rdocumentation.org
4-4. 1-SE rule (cp($\alpha$)값에 따른 가지치기 결정)
- $1-SE$ rule이란 의사결정나무가 갖는 minimum error에서 1 standard error를 더했을 값에 해당하는 tree를 최종 모델로 하는 것을 의미한다. (가장 낮은 오류보다 조금 덜 복잡한 의사결정나무를 선택한다).
$$1-SE~rule = Minimum~Error + Standard~Error$$
- 설명은 어렵지만 plotcp() 함수를 통해 시각화를 한다면 $1-SE$ rule에 해당하는 값은 수평선(점선)으로 시각화된다. 따라서 해당 점선을 기준으로 의사결정나무의 크기를 제한할 수 있다.
코드 실습 (plotcp())
4-2에서 생성한 모델 dt1의 plotcp() 결과를 확인한다.
plotcp(dt1)
위의 결과를 확인하면 대략 cp = 0.0017일 때 최적의 의사결정나무라 판단할 수 있다. 해당 지점은 size of tree = 26 이므로 다시 이야기하면 leaf node의 수가 26일 때 가장 적합한 의사결정나무라 할 수 있다. 이를 기준으로 가지치기(prune)을 적용하는 결과는 다음과 같다.
가지치기 적용
R에서 가지치기를 할 때에는 prune() 함수를 활용한다. 함수의 인자는 다음과 같다.

4-2에서 모델링한 dt1에 가지치기를 적용하여 새로운 모델 dt1_p를 생성하고 rpart.plot()을 통해 시각화 하면 다음과 같다.
# 가지치기 적용
# cp(alpha)값을 0.0017로 하여 가지치기를 진행한다.
dt1_p <- prune(dt1, cp = 0.0017)
# 결과 시각화
rpart.plot(dt1_p,
box.palette = list("lightblue",
"lightgreen",
"lightcoral",
"gray",
"pink",
"yellow",
"purple"),
cex = 0.35, # 글자의 크기를 조정한다.
extra=5) # 출력값의 유형이며 몇 개의 유형이 정해져 있다.
기존의 모델(좌측)과 prune을한 모델(우측)의 결과는 붉은 색 원 부분에서 두드러진다.
5. caret을 통한 예측모델 모델링하기
5-1. Modeling
# preprocessing
library(dplyr)
library(readr)
# vizualizing
library(ggplot2)
library(rpart.plot) # 학습한 tree 시각화
library(vip) # 변수 중요도 시각화
library(pdp) # 이번 실습에서는 사용하지 않는다. (이유는 후술)
# modeling
library(caret) # predict를 수행
library(rpart) # Decision tree 학습
# 데이터 불러오기-----------------------------------------------------------------
df <- read_csv("D:\\Data Science\\ADP\\Data 모음\\Obesity.csv")
# 결과변수의 비율을 유치한 채 데이터 분할 train : dev (8 : 2)
set.seed(123)
train_index <- createDataPartition(df$NObeyesdad, p = 0.7, list=FALSE)
# train set
df_train <- df[train_index,]
df_train <- df_train %>%
mutate(across(where(is.character), as.factor)) %>%
select(-id)
str(df_train)
# dev set
df_dev <- df[-train_index,] %>%
mutate(across(where(is.character), as.factor)) %>%
select(-id)
str(df_dev)
# Cross validation 설정----------------------------------------------------------
train_cv <- trainControl(
method = "cv",
number = 5,
savePredictions = "all", # 결과값 저장
# 모델 성능 평가지표 유형들을 결정한다.
# 현제는 multiClassSummary를 통해 다항분류의 경우에 해당한다.
# 이외에 이항분류와 회귀를 설정할 수 있다.
# 걱정할 필요없이 해당 인자를 설정하지 않아도 caret은 알아서 적합한 지표를 선택한다.
summaryFunction = multiClassSummary
)
# 모델 학습-----------------------------------------------------------------------
# Girdsearch 포함.
# caret을 사용할 경우 cp만을 튜닝할 수 있다.
# 다른 파라미터 튜닝을 원할경우 "mlr"과 같은 다른 패키기를 사용.
# cp를 튜닝하는 모델 생성
set.seed(123)
dt1_tune <- train(NObeyesdad ~ .,
data=df_train,
method = "rpart",
trControl = train_cv,
# caret에서는 cp만 지원한다.
# 다른 파라미터 튜닝을 위해서는 mlr 등의 패키지를 사용해야 한다.
tuneGrid = expand.grid(cp = seq(0.05, 0.2, 0.01)),
metric = "Accuracy")
# cp를 튜닝하지 않는 모델 생성
set.seed(123)
dt1_no_tune <- train(NObeyesdad ~ .,
data=df_train,
method = "rpart",
trControl = train_cv,
metric = "Accuracy")
# 학습 결과 확인
dt1_tune$bestTune
dt1_no_tune$bestTune
- 튜닝을 한 경우 가장 최소값(cp = 0.05)를 선택하고 튜닝을 하지 않은 경우 cp = 0.0844를 선택한다.
# 예측 수행-------------------------------------------------------------------------------------
# 변수들의 class imbalance 때문에 warning이 출력된다.
# 현제 모델링은 단순 실습이기에 그대로 진행한다.
pred1_tune <- predict(dt1_tune, newdata = df_dev)
pred1_no_tune <- predict(dt1_no_tune, newdata = df_dev)
# 학습 결과 평가 ---------------------------------------------------------------------------------
conf_matrix_tune <- confusionMatrix(pred1_tune, df_dev$NObeyesdad)
conf_matrix_no_tune <- confusionMatrix(pred1_no_tune, df_dev$NObeyesdad)
# 평가 지표 출력을 위한 함수 정의
# Accuracy, Average_precision, Average_recall, Average_F1score
eval_func <- function(conf_matrix){
class_metrics <- conf_matrix$byClass
accuracy <- conf_matrix$overall['Accuracy']
precision <- mean(ifelse(is.na(class_metrics[,'Pos Pred Value']), 0, class_metrics[,'Pos Pred Value']))
recall <- mean(ifelse(is.na(class_metrics[,'Sensitivity']), 0, class_metrics[,'Sensitivity']))
f1_score <- mean(ifelse(is.na(class_metrics[,'F1']), 0, class_metrics[,'F1']))
print(paste("Accuracy:", round(accuracy, 4)))
print(paste("Average Precision:", round(precision, 4)))
print(paste("Average Recall:", round(recall, 4)))
print(paste("Average F1 Score:", round(f1_score, 4)))
}
# 함수를 적용하여 평가 지표 출력
eval_func(conf_matrix_tune)
eval_func(conf_matrix_no_tune)
- 튜닝을 한 경우, 즉 cp값이 더 작은 경우 일반적으로 모든 면에서 모델의 성능이 더 좋아진다. 물론 데이터 분할을 하여 dev set에 적용한 결과이기에 test set에서의 결과는 달라질 수 있다.
5-2. 시각화를 통한 결과 해석
학습한 의사결정나무 시각화
# 결과 시각화 확인--------------------------------------------------------------
# CV와 cp를 튜닝하였기에 finalModel을 출력한다.
rpart.plot(dt1_tune$finalModel) # 튜닝을 하여 성능은 좋아지지만 복잡해진다.
rpart.plot(dt1_no_tune$finalModel) # 튜닝이 없으면 단순하지만 성능이 떨어진다.
변수 중요도 시각화
# 변수 중요도 확인
vip(dt1_tune) +
theme_minimal()
vip(dt1_no_tune) +
theme_minimal()
- VIP를 계산할 때의 기준은 reduction in the loss function 이다. 쉽게 표현하면 가장 분류에 많이 사용된 변수이다. (loss function의 감소가 가장 큰 변수로 분류하기 때문).
- caret을 활용할 경우 개별 값들은 표준화가 되어 가장 감소폭이 큰(중요한) 변수를 100으로 한다. 이후 나머지 변수들은 가장 중요한 변수에 대한 상대적 감소량으로 표현된다.
- 쉽게 말해 가장 감소량이 큰 변수를 기준으로 표준화를 하여 비교를 수행한다.
- 번외로 node 분류에는 사용되지 않았지만 분류 기준으로 고려되었던 경쟁력 있는 변수 또한 저장해 둔다. (분류 기준으로 채택 되지는 못하였지만 고려되었을 만큼 분류에 유의미하기 때문).
6. 번외 (회귀 & 이항분류)
- 의사결정나무를 rpart와 caret으로 수행할 경우 회귀문제와 이항분류문제는 실습에서 확인한 다항분류방식의 코드로 접근하면 된다. (대부분 rpart와 caret이 결과변수에 맞는 방법에 맞추어 자동적으로 모델링을 수행한다).
- 단, 주의해야할 부분이 있다면 결과의 해석에 있어서는 평가지표 또한 달라지기에 결과를 해석하는 과정에서는 조금 주의가 필요하다.
- 마지막으로 회귀와 이항분류의 결과를 확인할 때에는 앞서 후술한다 하였던 library(pdp)를 불러와 partial 함수를 사용할 수 있다. (Reference에 있는 <Hands on machine learning with R>의 하단부에서 해당 내용을 확인할 수 있다. 포스팅에서는 자세히 다루지 않는다).
- partial은 'Partial Dependence Plot'으로 개별 변수와 결과변수 간의 관계를 해석할 때 사용한다.
- 회귀분석에서는 correlation과 유사하다 볼 수 있지만 pdp는 예측에 미치는 영향인 반면 correlation은 상관관계를 기반으로 한다는 차이가 있다.
- 이항분류에서는 예측확률과 개별 변수의 관계를 확인할 수 있다.
- partial은 'Partial Dependence Plot'으로 개별 변수와 결과변수 간의 관계를 해석할 때 사용한다.
7. Reference
- Hands on machine learning with R PDF
https://bradleyboehmke.github.io/HOML/DT.html - Cross-entropy
https://www.datacamp.com/tutorial/the-cross-entropy-loss-function-in-machine-learning - Gini Index
https://medium.com/@ompramod9921/decision-trees-91530198a5a5 - rpart::rpart() doc
https://www.rdocumentation.org/packages/rpart/versions/4.1.23/topics/rpart - rpart.control doc
https://www.rdocumentation.org/packages/rpart/versions/4.1.23/topics/rpart.control - kaggle 데이터
https://www.kaggle.com/competitions/playground-series-s4e2/data?select=train.csv - rpart.plot::rpart.plot() doc
https://www.rdocumentation.org/packages/rpart.plot/versions/3.1.2/topics/rpart.plot - 구체적인 rpart 문서 (cran)
https://cran.r-project.org/web/packages/rpart/vignettes/longintro.pdf - caret에서 grid search를 지원하는 파라미터는 cp하나이다. 다른 파라미터 튜닝은 mlr 등 다른 워크 프레임을 사용해야 한다.
https://stackoverflow.com/questions/36802846/how-to-tune-multiple-parameters-using-caret-package
'♧ Machine learning' 카테고리의 다른 글
| [ML] Mhachine learning workflow (0) | 2024.07.26 |
|---|